Bird_Formation
Photo by Ethan Weil on Unsplash

Multiplex Information Networks for Formation Control


R esearch ideas in the multiagent system field come from observing nature. For example, we can see migrating birds flying in V-shaped formation to reduce the drag force and save energy for the long trips, ants working together to find and transport food back to their nest or fish swimming in schools not only to increase their sensing capability but also to confuse their predator, and hence boost survival rates. The advantages of these "teamwork" in nature are the main motivation for multiagent system algorithms and applications. Specifically, algorithms are developed for a group of robots or vehicles (called agents) so that they can communicate, collaborate, and coordinate with each other to achieve a global task. One branch of multiagent systems is formation control where controllers are designed to allow vehicles to form and maintain the desired formation under adverse conditions and dynamic environment.

Formation control has a wide range of applications such as satellite clusters, search and rescue missions, security patrol, automated highway systems to name but a few. As an illustration, a group of quadcopters can be equipped with lifesavers and deployed in formation (to increase the observation field) at a pool or a beach to monitor and help swimmers in case of accidents. This also includes searching for a missing person in an area and drop a lifesaver if found. Therefore, formation control promises a bright future where autonomous vehicles can operate along the side human to provide us convenience as well as safety.

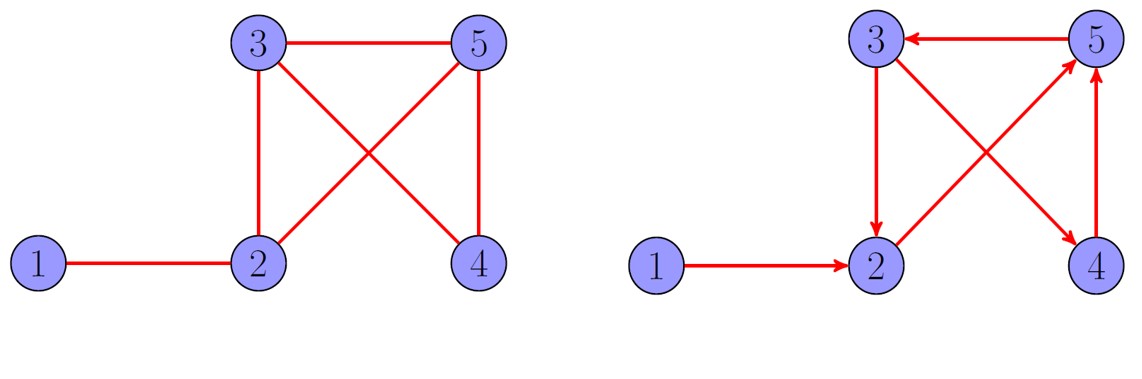
Graph
Photos on robots.net
Figure 1 - An application of formation control.

The most important tool to develop algorithms for multiagent systems is graph theory, which allows a multiagent system to be represented by a graph. Particularly, each agent is denoted by a circle, and communication between agents is denoted by edges as illustrated in Figure 1. It can be either two-way communication (undirected graph) or one-way communication (directed graph).

Graph
Figure 2 - A multiagent system with 5 agents is represented by an undirected graph (left) and directed graph (right).

Algorithms for multiagent systems are developed based on the philosophy that agents have to reach consensus on some quantities in order to achieve a global task. For example, in formation control, if each agent knows its current position and its reference point in the formation, then they can measure the displacement (distance and direction) between themselves and the reference point. By exchanging the current position information with neighboring agents, eventually agents in the system can adjust themselves to reach consensus on the displacement (denoted by \(\tau^*\) in Figure 2). When the consensus is reached, the formation is accomplished. This method is called displacement-based formation control.

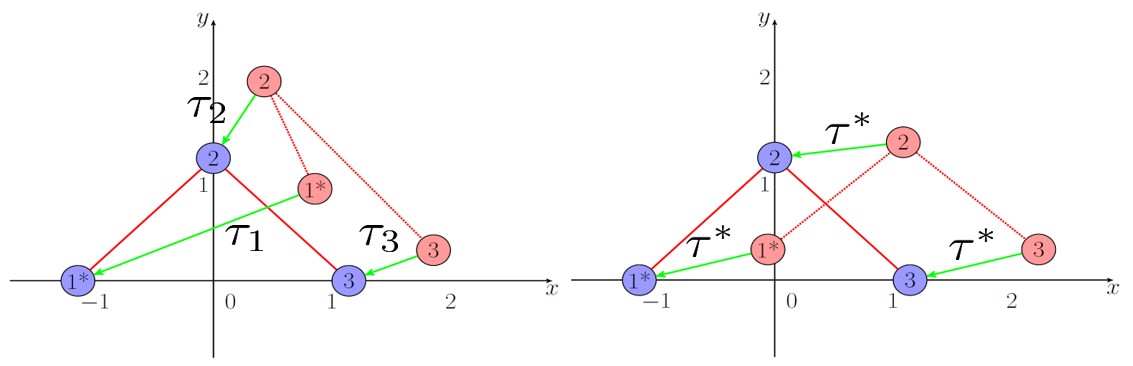
Formation
Figure 3 - Current positions of agents are denoted by red, and reference points in the formation are denoted by purple. Through exchanging information, agents reach consensus on the displacement, and hence the formation is accomplished.

A limitation of displacement-based formation control is that once the formation is formed, it is fixed; that is, the formation size and orientation cannot be changed. Under the dynamics environment, the formation may be required to change their size and orientation. For instance, the formation needs to scale down to pass through a narrow passage. This can be done if there is an intelligent agent (called the leader) in the system that can calculate/know the desired scaling factor and the rotation angle for the formation and distributed this information to the whole network. Since most of the current literature on formation control utilize only a single layer of consensus for formation control, the only feasible way to do this is to make the leader be able to communicate and/or broadcast the information to the whole network on the desired scaling factor and rotation angle. This centralized communication requires a large communication bandwidth, and it becomes infeasible when the number of agents in the system is large.

To work around this limitation, multiplex information networks is a solution. Multiplex information network allows the formation to be able to change size and orientation in a decentralized manner. The idea of a multiplex information network is to utilize multiple layers of consensus in parallel for distributing the information. That is, besides the main layer exchanging position information to form the formation, consensus layers are utilized to spread out the desired parameters such as the scaling factor, the rotation angle, and maybe other information from the leader to all agents in the system. This information will be updated and affect the main layer, and hence altering the formation as desired. With this methodology, the leader is only required to communicate with its neighboring agents.

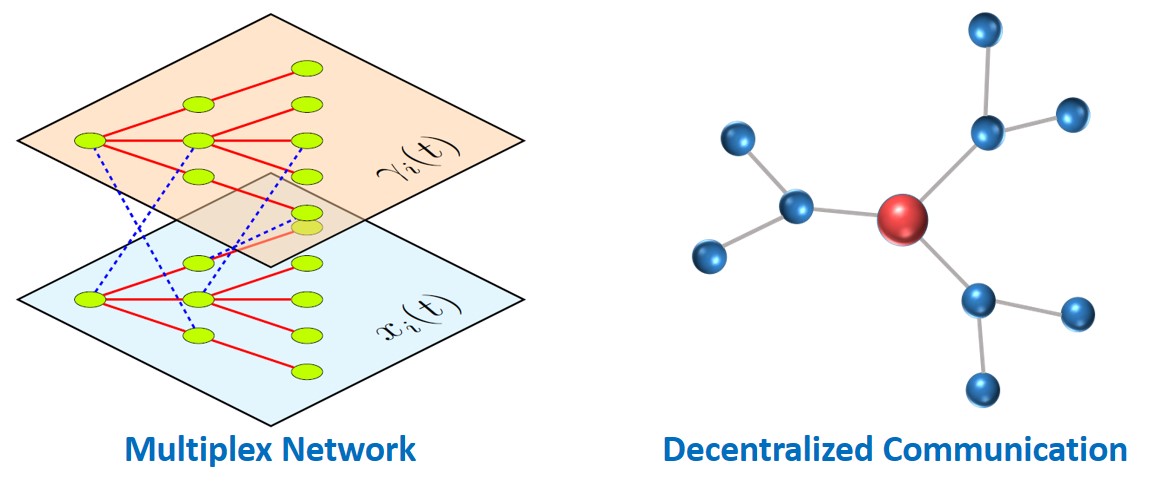
Multiplex
Figure 4 - Multiplex Information Networks utilize multiple layers of consensus and allow decentralized communication.

Our research on utilizing a multiplex information network for formation control focuses not only on forming the formation, tracking a dynamics target but also on allowing the formation size and orientation to be controlled via the leader. In addition, potential energy functions are added to the algorithms for collision avoidance and connectivity maintenance purposes. The two videos below justify the efficacy of the algorithms. For interested reader, the algorithms are presented in our papers C-01), C-02) and C-03).